1. Stochastic
Steepest Ascent는 너무 Greedy한 알고리즘이다. 즉 너무 현재상태에서만 좋은 값을 구하려고 한다.
그래서 초기값에 따라 너무 의존적으로 local에 빠지기 쉽다.
Stochastic은 neighbors를 구할 때 확률적인 요소를 추가하여 항상 best한 이웃을 구하는 것이 아닌, 조금 안 좋은 이웃을 선택할 수 있다.
그렇게 구한 neighrbor의 value와 current value를 비교하여 더 좋으면 update한다.

어떻게 확률적으로 이동하는지는 아래에서 살펴보자.
1) 현재 위치를 random으로 초기화
2) 현재 위치의 value 계산
while:
3) 현재 위치를 기준으로 모든 neighbors를 구함.
4) neighbors 중 stochasticBest를 통해 successor를 구함.
5) successor value와 current value 비교
def stochastic(p):
current = randomInit(p)
valueC = evaluate(current, p)
i = 0
while i < LIMIT_STUCK:
neighbors = mutants(current, p)
(successor, valueS) = stochasticBest(neighbors, p)
if valueS < valueC:
current = successor
valueC = valueS
i = 0
else:
i+=1
return current, valueC
Steepest Ascent와 first choice를 조금 섞은 알고리즘을 볼 수 있다.
중요하게 볼 것은 stochasticBest 함수다. 이를 통해 확률적으로 successor를 결정한다.
2. Numeric
1) randomInit : 현재 위치를 random으로 초기화
def randomInit(p):
"""
p : [expr, [varNames, low, up]]
varNames : [x1, x2, x3 . .]
low : [-30, -30, . . .]
up : [30, 30, . . .]
"""
varNames = p[1][0]
low = p[1][1]
up = p[1][2]
init = []
for i in range(len(varNames)):
val = random.randint(int(low[i]), int(up[i]))
init.append(val)
return init # 초기값 : [-10, 21, 3, 17, -28]
가장 처음에 현재 위치를 random하게 초기화하는 함수다.
단순하게 for문을 돌면서 각 value에 -30, 30사이의 수를 리스트에 담아 return 한다.
2) evaluate : 현재 위치의 value 계산
def evaluate(current, p): # current : [-10, 21, 3, 17, -28]
"""
NumEval : 계산 횟수를 세기 위한 변수
expr : (x1 - 2) ** 2 +5 * (x2 - 5) ** 2 + 8 * (x3 + 8) ** 2 + 3 * (x4 + 1) ** 2 + 6 * (x5 - 7) ** 2
valNames : [x1, x2, . . .]
"""
global NumEval
NumEval += 1
expr = p[0]
varNames = p[1][0]
for i in range(len(varNames)):
assignment = varNames[i] + '=' + str(current[i])
exec(assignment, globals())
return eval(expr) # value
for문을 통해 exec를 실행시키면 다음과 같이 변수에 값을 넣는다.
x1=-10
x2=21
x3=3
x4=17
x5=-28
이후 eval을 통해 expr에 각 변수를 대입하여 value를 return 한다.
3) mutants : 현재 위치를 기준으로 모든 neighbors를 구함.
def mutants(current, p): # current : [-10, 21, 3, 17, -28]
neighbors = []
for i in range(len(current)):
# 각 변수에 대해 DELTA를 더하고 빼서 이웃을 생성
# DELTA : 0.01
neighbors.append(mutate(current, i, DELTA, p))
neighbors.append(mutate(current, i, -DELTA, p))
return neighbors # [[-9.99, 21, 3, 17, -28], [-10.01, 21, 3, 17, -28], [-10, 21.01, 3, 17, -28], [-10, 20.99, 3, 17, -28] . . . ]
def mutate(current, i, d, p):
curCopy = current[:]
domain = p[1] # [VarNames, low, up]
l = domain[1][i] # Lower bound of i-th
u = domain[2][i] # Upper bound of i-th
if l <= (curCopy[i] + d) <= u:
curCopy[i] += d
return curCopy
mutants함수를 통해 현재 위치에서 각각의 변수(x1 ~ x5)마다 neighbors를 생성한다.
이웃은 현재 위치에서 DELTA만큼 더하고 뺀 위치가 neighbors가 된다.
변수가 5개이므로 총 10개의 neighbors가 만들어진다.
4) stochasticBest : neighbors 중 stochasticBest를 통해 successor를 구함.
def stochasticBest(neighbors, p):
"""
neighbors : [[-9.99, 21, 3, 17, -28], [-10.01, 21, 3, 17, -28], [-10, 21.01, 3, 17, -28], [-10, 20.99, 3, 17, -28] . . . ]
p : [expr, [varNames, low, up]]
varNames : [x1, x2, x3 . .]
low : [-30, -30, . . .]
up : [30, 30, . . .]
"""
# Smaller valuse are better in the following list
valuesForMin = [evaluate(indiv, p) for indiv in neighbors] # 각 이웃에 대한 value가 저장됨 10개
# [2709.223678603643, 2708.551898233208, 2709.1711718148663, 2708.605205021985, 2707.0073816895265, 2710.7695951473243, 2707.9149591987834, 2709.8610176380676, 2709.9749383211883, 2707.801638515663]
largeValue = max(valuesForMin) + 1 # valuesForMin 중에 가장 높은 value에서 + 1
valuesForMax = [largeValue - val for val in valuesForMin] # valuesForMin의 각 값에 largeValue 빼기
# [2.5459165436814146, 3.217696914116459, 2.598423332457969, 3.164390125339196, 4.76221345779777, 1.0, 3.8546359485408175, 1.9085775092567019, 1.7946568261359062, 3.967956631661309]
# Now, larger values are better
total = sum(valuesForMax) # 28.814467288987544
randValue = random.uniform(0, total)
s = valuesForMax[0]
for i in range(len(valuesForMax)):
if randValue <= s: # The one with index i is chosen
break
else:
s += valuesForMax[i+1]
return neighbors[i], valuesForMin[i] # i에 해당하는 neighbors랑 그때의 value
이 부분이 가장 중요한 부분이다.
valuesForMin을 통해 neighbors의 모든 value를 받은 후 valuesForMax를 통해 수를 단순화한다.
stochastic 즉 확률적인 요소를 결정하는 것은 바로 randValue이다. 0부터 total 사이의 숫자를 random하게 결정하면서 항상 가장 좋은 best를 뽑는 것이 아니라, 확률적으로 결정한다.
만약 randValue를 8이라고 가정해보자.
| i | randValue | s | valuesForMax |
| 0 | 8 | 2.54 | 2.54 |
| 1 | 8 | 5.75 | 3.21 |
| 2 | 8 | 8.34 | 2.59 |
| 3 | 8 | - | - |
=> neighbors[2], valuesForMin[2]가 return 된다.
이렇게 항상 좋은 best를 return하는 것이 아닌, 확률적으로 선택한다.
5) current value와 successor value를 비교
while i < LIMIT_STUCK:
neighbors = mutants(current, p)
(successor, valueS) = stochasticBest(neighbors, p)
if valueS < valueC:
current = successor
valueC = valueS
i = 0
else:
i+=1
6) 실행결과
- Convex

- Griewank

- Ackley

3. TSP
Tsp에서 도시 수가 30일 때로 문제를 풀어보자
30
(8, 31)
(54, 97)
(50, 50)
(65, 16)
(70, 47)
(25, 100)
(55, 74)
(77, 87)
(6, 46)
(70, 78)
(13, 38)
(100, 32)
(26, 35)
(55, 16)
(26, 77)
(17, 67)
(40, 36)
(38, 27)
(33, 2)
(48, 9)
(62, 20)
(17, 92)
(30, 2)
(80, 75)
(32, 36)
(43, 79)
(57, 49)
(18, 24)
(96, 76)
(81, 39)
첫 번째 줄에는 도시 수를 나타내고
두 번째 줄부터는 도시의 좌표이다.
Tsp 문제도 numeric와 같은 알고리즘으로 구현된다. 하지만 각 function의 세세한 내용이 다르다.
0) 문제를 생성할 때 각 도시마다의 거리 table을 생성
def calcDistanceTable(numCities, locations):
"""
numCities : 30
locations : [[8, 31], [54, 97], [50, 50] . . .]
"""
table = [[0] * numCities for i in range(numCities)]
for i in range(numCities):
for j in range(i+1, numCities):
x1, y1 = locations[i]
x2, y2 = locations[j]
distance = math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
table[i][j] = distance
table[j][i] = distance
return table
"""
table 출력
[[0,80.44874144447506, 46.09772228646444, 58.9406481131655, . . . ],
[80.44874144447506, 0, 47.16990566028302, 81.74350127074322, 52.49761899362675, . . .],
...
... ]
"""
각 도시마다의 거리를 저장한 table이다.
1번 도시를 기준으로 2, 3, 4, ... , 30 도시의 거리
2번 도시를 기준으로 1, 3, 4, ... , 30 도시의 거리
.
.
30번 도시를 기준으로 1, 2, 3, ... , 29 도시의 거리
1) randomInit : 현재 위치를 random으로 초기화
def randomInit(p):
"""
p : [numCities, locations, table]
numCities : 30
locations: [[8, 31], [54, 97], [50, 50] . . .]
table : 각 도시마다의 거리 테이블
"""
n = p[0]
init = list(range(n))
random.shuffle(init)
return init # [29, 20, 12, 15, 24, 4, 14, 2, 27, 16, 21, 3, 26, 1, 0, 8, 9, 28, 10, 7, 23, 17, 18, 19, 13, 25, 5, 11, 6, 22]
random하게 초기 도시 순서 결정한다.
2) evaluate : 현재 위치의 value 계산
def evaluate(current, p):
"""
current : [29, 20, 12, 15, 24, 4, 14, 2, 27, 16, 21, 3, 26, 1, 0, 8, 9, 28, 10, 7, 23, 17, 18, 19, 13, 25, 5, 11, 6, 22]
p : [numCities, locations, table]
"""
global NumEval
NumEval += 1
n = p[0]
table = p[2]
cost = 0
for i in range(n-1):
locFrom = current[i]
locTo = current[i+1]
cost += table[locFrom][locTo]
cost += table[current[-1]][current[0]]
return cost # 총 거리수
도시마다의 거리를 다 더한값인 cost를 return한다.
3) mutants : 현재 위치를 기준으로 모든 neighbors를 구함.
def mutants(current, p):
n = p[0]
neighbors = []
count = 0
triedPairs = []
while count <= n:
i, j = sorted([random.randrange(n) for _ in range(2)])
if i < j and [i, j] not in triedPairs:
triedPairs.append([i, j])
curCopy = inversion(current, i, j)
count += 1
neighbors.append(curCopy)
return neighbors
def inversion(current, i, j):
curCopy = current[:]
while i < j:
curCopy[i], curCopy[j] = curCopy[j], curCopy[i]
i += 1
j -= 1
return curCopy
neighbors를 생성할 때 i, j를 random하게 뽑은 후 현재 state의 i ~ j 를 inversion한 것을 neighbor이라고 한다.
밑의 예시를 통해 보자.
첫 번째 neighrbor은 현재 state([29, 20, 12, 15, 24, 4, 14, 2, 27, 16, 21, 3, 26, 1, 0, 8, 9, 28, 10, 7, 23, 17, 18, 19, 13, 25, 5, 11, 6, 22])에서 16 ~ 19번째를 inversion한 것이다.
총 31개의 neighbors를 구한다.
neighbors 출력
[[29, 20, 12, 15, 24, 4, 14, 2, 27, 16, 21, 3, 26, 1, 0, 8, 9, 23, 7, 10, 28, 17, 18, 19, 13, 25, 5, 11, 6, 22],
[29, 20, 12, 15, 24, 4, 14, 2, 27, 10, 28, 9, 8, 0, 1, 26, 3, 21, 16, 7, 23, 17, 18, 19, 13, 25, 5, 11, 6, 22],
[29, 24, 15, 12, 20, 4, 14, 2, 27, 16, 21, 3, 26, 1, 0, 8, 9, 28, 10, 7, 23, 17, 18, 19, 13, 25, 5, 11, 6, 22],
[29, 15, 12, 20, 24, 4, 14, 2, 27, 16, 21, 3, 26, 1, 0, 8, 9, 28, 10, 7, 23, 17, 18, 19, 13, 25, 5, 11, 6, 22],
.
.
.]
4) neighbors 중 stochasticBest를 통해 successor를 구함.
def stochasticBest(neighbors, p):
"""
neighbors : 총 31개의 neighbors
p : [numCities, locations, table]
numCities : 30
locations: [[8, 31], [54, 97], [50, 50] . . .]
table : 각 도시마다의 거리 테이블
"""
# Smaller valuse are better in the following list
valuesForMin = [evaluate(indiv, p) for indiv in neighbors] # 각 이웃에 대한 value가 저장됨 31개
# [1463.2432289381327, 1472.5383654210098, 1482.751305400727, 1459.1988259423174, ...]
largeValue = max(valuesForMin) + 1 # valuesForMin 중에 가장 높은 value에서 + 1
valuesForMax = [largeValue - val for val in valuesForMin] # valuesForMin의 각 값에 largeValue 빼기
# [126.80665423241112, 117.51151774953405, 107.2985777698168, 130.8510572282264, ...]
# Now, larger values are better
total = sum(valuesForMax) # 3233.4632863888137
randValue = random.uniform(0, total)
s = valuesForMax[0]
for i in range(len(valuesForMax)):
if randValue <= s: # The one with index i is chosen
break
else:
s += valuesForMax[i+1]
return neighbors[i], valuesForMin[i] # i에 해당하는 neighbors랑 그때의 value
Numeric과 동일하게 작동하여 확률적으로 neighbors를 선택한다.
5) current value와 successor value를 비교
while i < LIMIT_STUCK:
neighbors = mutants(current, p)
(successor, valueS) = stochasticBest(neighbors, p)
if valueS < valueC:
current = successor
valueC = valueS
i = 0
else:
i+=1
6) 실행결과
- tsp30
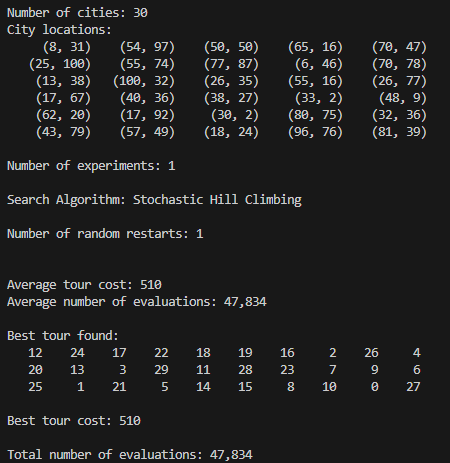
- tsp50

- tsp100

First choice와 steepest ascent와 다르게 이웃 중에서 가장 좋은 값이 아니라 확률적으로 successor를 선택하는 알고리즘이다.
이를 통해 초기값에 의존도가 떨어지고 local min에 빠질 확률이 조금 줄어든다.
한줄요약
Stochastic : 확률적으로 이웃을 선택하여 그 value와 현재 value를 비교하여 좋은 쪽으로 이동하며 local min을 찾는 알고리즘
'인공지능 > Local Search Algorithms' 카테고리의 다른 글
| [Local Search Algorithms] Gradient Descent (1) | 2024.12.07 |
|---|---|
| [Local Search Algorithms - Meta Heuristic Algorithm] Simulated Annealing (0) | 2024.12.06 |
| [Local Search Algorithms - Hill climbing Algorithms] First Choice (0) | 2024.12.04 |
| [Local Search Algorithms - Hill climbing Algorithms] Steepest Ascent (0) | 2024.12.01 |
| [Local Search Algorithms] - 개요 (2) | 2024.12.01 |