1. Gradient Descent
gradient descent는 기울기를 이용하여 min을 찾는 알고리즘이다.
현재 state에서의 기울기를 계산하여 현재 위치에서 그 기울기만큼 뺀 것을 다음 state로 update하는 알고리즘이다.
만약 기울기가 음수이면, state가 양수방향으로 update되면서 local min에 다가갈 수 있고, 기울기가 양수면 state가 음수방향으로 update되면서 local min에 다가갈 수 있다.

이때 알파는 learning rate다.
learning rate가 크면 min으로 가는 step이 크지만, 수렴하는 것이 아닌 발산할 수 있다.
learning rate가 작으면 수렴할 가능성이 크지만, 시간이 오래걸리는 단점이 있다.

1) 현재 위치를 random으로 초기화
2) 현재 위치의 value 계산
while:
3) 현재 위치로부터 다음 step을 계산
4) nextP의 value 계산
5) next value와 current value 비교
def gradientDescent(p):
currentP = randomInit(p) # Current point
valueC = evaluate(currentP, p)
while True:
nextP = takeStep(currentP, valueC, p)
valueN = evaluate(nextP, p)
if valueN >= valueC:
break
else:
currentP = nextP
valueC = valueN
return currentP, valueC
gradinet descent는 이웃을 구하는 것이 아닌 takeStep을 통해 기울기를 뺀 다음 state로 이동하는 것이다.
또한 gradient descent는 TSP문제는 해결 못하고 Numeric 문제만 해결할 수 있다.
2. Numeric
Convex로 문제를 풀어보자.
(x1 - 2) ** 2 +5 * (x2 - 5) ** 2 + 8 * (x3 + 8) ** 2 + 3 * (x4 + 1) ** 2 + 6 * (x5 - 7) ** 2
x1,-30,30
x2,-30,30
x3,-30,30
x4,-30,30
x5,-30,30
1) randomInit : 현재 위치를 random으로 초기화
def randomInit(p):
"""
p : [expr, [varNames, low, up]]
varNames : [x1, x2, x3 . .]
low : [-30, -30, . . .]
up : [30, 30, . . .]
"""
varNames = p[1][0]
low = p[1][1]
up = p[1][2]
init = []
for i in range(len(varNames)):
val = random.randint(int(low[i]), int(up[i]))
init.append(val)
return init # [-10, 21, 3, 17, -28]
2) evaluate : 현재 위치의 value 계산
def evaluate(current, p): # current : [-10, 21, 3, 17, -28]
"""
NumEval : 계산 횟수를 세기 위한 변수
expr : (x1 - 2) ** 2 +5 * (x2 - 5) ** 2 + 8 * (x3 + 8) ** 2 + 3 * (x4 + 1) ** 2 + 6 * (x5 - 7) ** 2
valNames : [x1, x2, . . .]
"""
global NumEval
NumEval += 1
expr = p[0]
varNames = p[1][0]
for i in range(len(varNames)):
assignment = varNames[i] + '=' + str(current[i])
exec(assignment, globals())
return eval(expr) # value
3) takeStep : 현재 위치로부터 다음 step을 계산
def takeStep(x, v, p):
# 현재 위치 x에서 함수 값을 v로 사용하여 기울기(Gradient) 계산
grad = gradient(x, v, p) # 기울기
# 새로운 위치 계산하기
new_x = []
for xi, gi in zip(x, grad):
new_x_i = xi - alpha * gi # alpha : 0.01
new_x.append(new_x_i)
# 계산된 새로운 위치가 유효한 범위 안에 있는지 확인
if isLegal(new_x, p):
return new_x
else:
return x
def isLegal(x, p):
# 도메인 내에 있는지 확인
for xi, lower, upper in zip(x, p[1][1], p[1][2]):
if not (lower <= xi <= upper):
return False
return True
def gradient(x, v, p):
grad = []
for i in range(len(x)):
xCopyH = x[:]
xCopyH[i] += dx
g = (evaluate(xCopyH, p) - v) / dx # dx : 10 ** (-4)
grad.append(g)
return grad # 기울기 [0.04258637595455639, 0.09004706395643325, 0.735415186952082, 0.3067720192007073, 0.7318296405145475]
takeStep을 통해 다음 state의 위치를 return 한다.
gradient을 통해 현재 state의 기울기를 계산한 후 각 state마다 gradient descent 공식에 따라 다음 state를 계산한다.
isLegal을 도메인 내에 있는지 확인한다.
4) nextP의 value 계산
evaluate를 사용하여 3)에서 구한 nextP의 value를 계산한다.
5) next value와 current value 비교
if valueN >= valueC:
break
else:
currentP = nextP
valueC = valueN
value를 비교하여 state를 업데이트한다.
6) 실행 결과
- Convex

- Griewank
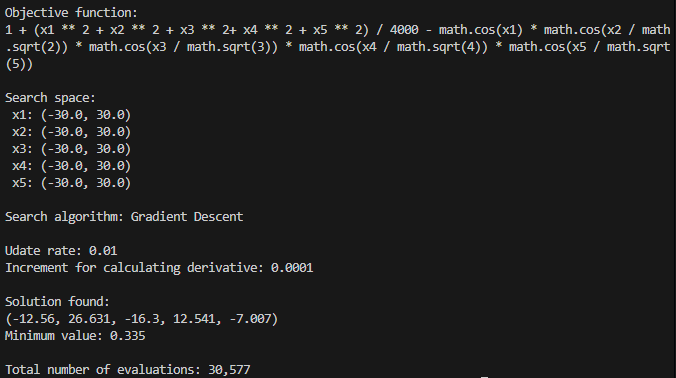
- Ackley

Hill Climbing과 Meta Heuristic 알고리즘과 다르게 neighbors를 구하는 것이 아니라, takeStep을 통해 기울기를 계산해서 다음 state를 결정하는 알고리즘이다.
이때문에 연속함수 문제만 구할 수 있고, TSP 문제는 구할 수 없다.
한줄요약
Gradient Descent : 현재 state에서 기울기만큼 빼면서 state를 update하는 알고리즘